时间/空间复杂度
时间复杂度是用来表示某一特定算法的所需时间的一种方法,它所代表的是算法中需要进行的基本计算的步骤的多少,但为什么要搞的那么复杂?为什么不直接使用时间来度量呢?
如果我们直接使用时间来度量算法之间的快慢,会发现相同的算法在不同的硬件环境下,所使用的时间并不相同,正如人力计算和机器计算的区别,拿一个深度学习的算法让人力进行计算,很可能需要几百年,几万年甚至更高,但一台超级计算机则可以在几天,甚至几分钟的时间内得到结果,这就是硬件环境带来的差异,但实际上计算量是相同的。
于是就提出了时间复杂度的概念,直接将算法中的基本运算的多少进行统计,用以表示一个算法的复杂程度。
所谓基本运算,比如加法,就是一个基本运算,对应的还有减法,乘法,除法,判断等。
- 执行时间:时间复杂度
- 内存消耗:空间复杂度
时间复杂度与空间复杂度的前面还有一个词,叫渐进,它表示的是:算法在输入数据的规模成倍增长的时候,相应的时间消耗多增长了多少。
渐进表示法
我们通常使用渐进符号来描述一个算法的复杂度。
大 Θ 符号
对于给定的一个函数$g(n)$,$f(n) = Θ(g(n))$,使得$c1 g(n) <= f(n) <= c2 g(n)$。
也就是说,存在的两个参数让$f(n)$保持在$c1 g(n)$与$c2 g(n)$之间。他给了我们一个上下界。
大 O 符号
如果我们只有一个函数的渐进上界的时候,我们使用 大O 符号。即$0 <= f(n) <= c g(n);f(n) = O(g(n))$
研究时间复杂度时通常会使用 大O 符号,因为我们关注的通常是程序用时的上界,而不关心其用时的下界。
大 Ω 符号
使用 Ω 符号来描述一个函数的渐进下界。即$0 <= c g(n) <= f(n);f(n) = Ω(g(n))$。
小 o 符号
如果说 大O 符号相当于小于等于号,那么 o oo 符号就相当于小于号。即$0 <= f(n) < c g(n);f(n) = o(g(n))$。
小 ω 符号
如果说 Ω 符号相当于大于等于号,那么 ω 符号就相当于大于号。即$0 <= f(n) < c g(n);f(n) = ω(g(n))$。
举个例子就可以很快的理解这一概念:
比如某个算法的时间复杂度是:
其中n代表数据量。
发现高次项随着数据量的少幅度改变就会让时间复杂度发生大幅度的改变,比如数据量n从1000提高到1001,那么高次项就增加了$1001^3 - 1000^3 = 30013001$,而二次项则是$1001^2 - 1000^2 = 2001$,一次项为$1001 - 1000 = 1$,常数项不改变。
在这种情况下,我们说高次项对时间复杂度的影响更大,而低次项则可以被忽略,于是,我们可以将上述时间复杂度变成:
现在,我们发现高次项前面的系数并不特别影响时间复杂度所在的数量级,于是就将系数也省去,最后时间复杂度变为:
但是怎么知道这个是代表时间复杂度呢?那就在前面加个大O吧,于是就有了大O表示法:
这样,我们就得到了这个算法的时间复杂度了。
最坏时间复杂度
时间复杂度实际上还分为最优时间复杂度,最坏时间复杂度,平均时间复杂度。
- 最优时间复杂度:算法完成工作最少需要多少基本操作。
- 平均时间复杂度:算法完成工作平均需要多少基本操作。
- 最坏时间复杂度:算法完成工作最多需要多少基本作。
最坏时间复杂度提供了一种保证,表明算法在此种程度的基本操作中一定能完成工作。因此,我们主要关注算法的最坏情况,一般在说到时间复杂度时,我们说的都是最坏时间复杂度。
时间复杂度的几条基本计算规则
- 基本操作,即只有常数项,认为其时间复杂度为$O(1)$
- 顺序结构,时间复杂度按加法进行计算。比如一个算法复杂度为$O(n)$的结构和一个算法复杂度为$O(n^2)$的结构相加,即$O(n^2 + n)$,简化为$O(n^2)$
- 循环结构,时间复杂度按乘法进行计算,比如外层循环为进行n次,内层为从0加到100,那么内层的时间复杂度为$O(100)$,外层要进行n次,则总体的时间复杂度为$O(100n)$,简化为$O(n)$。
- 分支结构,时间复杂度取最大值
常见时间复杂度
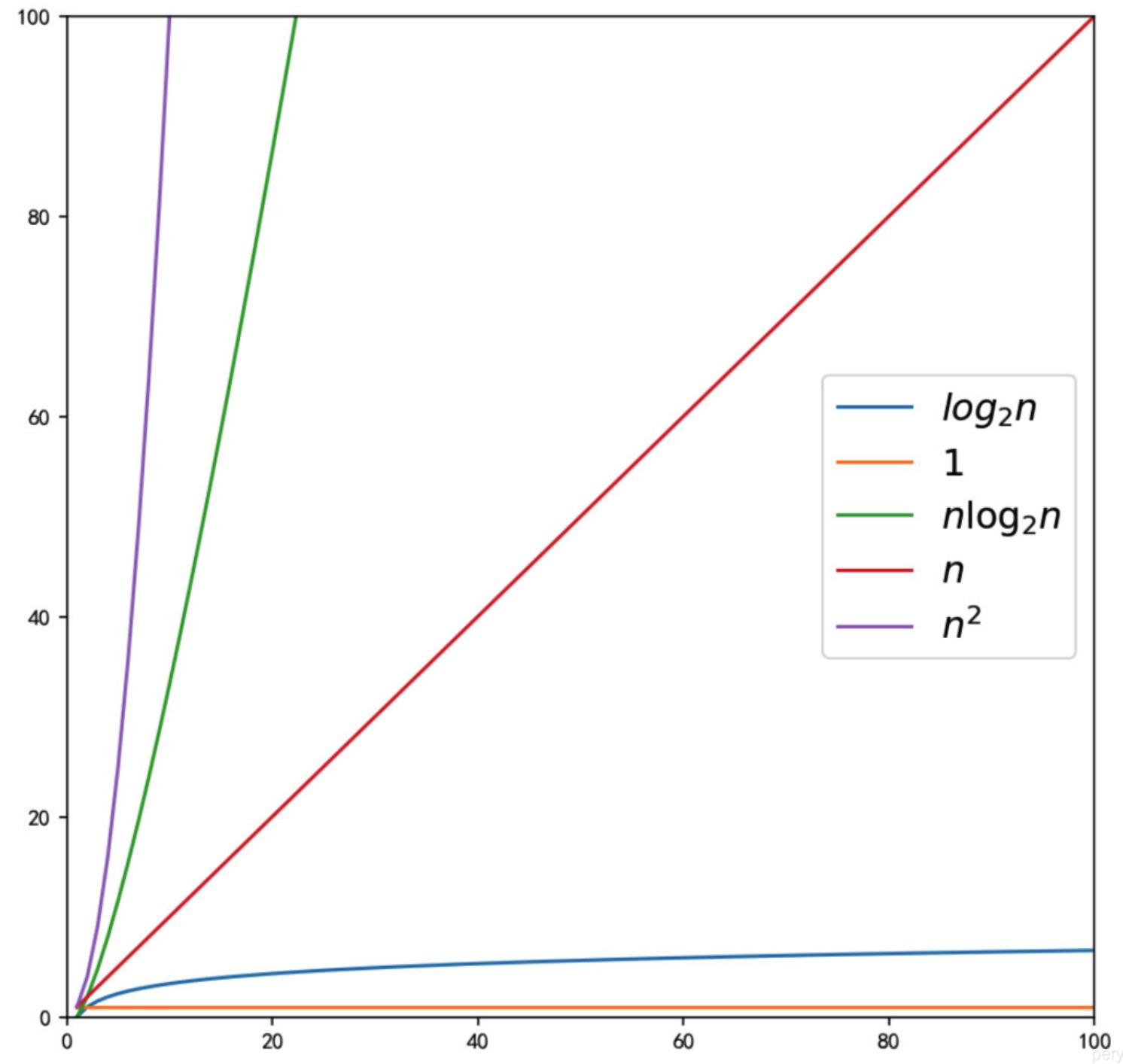
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
主定理
在时间复杂度的计算中,有一类问题的计算比较困难,这种问题就是递归问题,比如对于归并排序(Merge Sort)来说,每一层的复杂度为:
其中T(n)代表了当前层的时间复杂度,代表了将当前层的数据进行分解和将返回当前层的数据进行合并所需要的时间复杂度。
在递归问题中,时间复杂度计算的难点在于,如果要计算当前层,就需要首先得到下一层的时间复杂度,而为了计算下一层,又要计算下下层的时间复杂度,这就造成了计算困难。
为了能够快速得到递归算法的时间复杂度,可以使用主定理:
其中,
- n是问题规模大小,
- a是原问题的子问题个数,
- n/b是每个子问题的大小,这里假设每个子问题有相同的规模大小,
- f(n^d)是将原问题分解成子问题和将子问题的解合并成原问题的解的时间。
根据主公式定理,我们可以得到如下的结果:
上式的意思如下:我们可以将d看做代表了主公式中的第二项,即将原问题分解成子问题和将子问题的解合并成原问题的解的时间。
将$log_b a$看做代表了主公式中的第一项,即解决当前层问题所需要的时间复杂度。
如果$d > log_b a$,可以认为是解决当前层的时间复杂度的次数低于将原问题分解成子问题和将子问题的解合并成原问题的解的时间,于是我们可以直接使用第二项作为我们的时间复杂度。
如果$d = log_b a$,可以认为两者相等,则需要将两者都考虑进去。
如果$d < log_b a$,可以认为解决当前层的时间复杂度的次数更高,则直接使用第一项作为我们的时间复杂度。