红黑树

算法算法

Created At : 2023-07-31 20:11

Views 👀 :

Comment:

简介
红黑树规则特点
自底向上的插入
自顶向下的红黑树
自顶向下的删除
确定性跳跃表

简介

历史上，红黑树是AVL树的一个变种。对红黑树的操作在最坏情况下花费O(long N)时间，并且可以看到（对于插入操作的）一种审慎的非递归实现可以相对容易的完成（与AVL数相比）。

红黑树规则特点

每一个节点为红色，或者黑色。
根是黑色的。
如果一个节点是攻色那么子节点必是黑色。
从一个节点到一个null引用的每一条路径必须包含相同数目的黑色节点。

着色法则的一个结论是，红黑树的高度最多是2log(N+1)。因此，查找操作保证是一种对数的操作。

困难在于将一个新项插入到树中。通常把新项作为树叶放到树中。如果将它涂成黑色那么会违反条件4，因为将会建立一条更长的黑节点路径。因此这一项必须涂成红色。
如果他的父节点是黑色的，则插入完成。如果他的父节点是红色的，那么得到了连续的红色节点，这就违反了条件3。
此时我们必须要调整该树。用于完成这项任务的基本操作是颜色的改变和树旋转。

自底向上的插入

如果新插入的项的父节点是黑色的，那么插入完成。因此将25插入到图中的树中是简单的操作。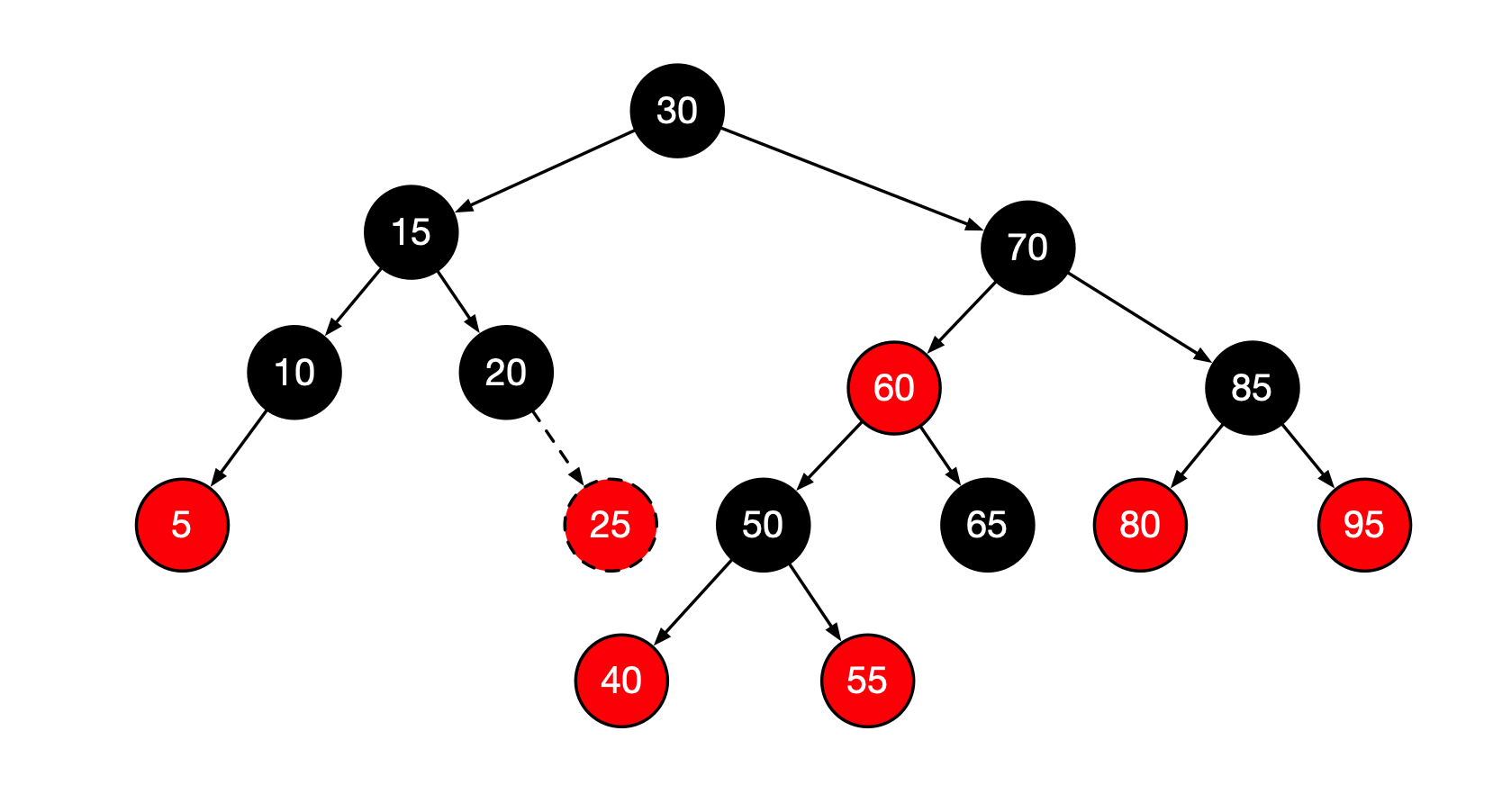
github

如果父节点是红色的，那么有几种情况（每种都有一个镜像对称）需要考虑。
首先，假设这个父节点的兄弟是褐色的（我们采纳规定：null节点都是黑色的）。
这对于插入3或8是适用的，但对插入99不适用。令X是新添加的树叶，P是他的父节点，S是父节点的兄弟（若存在），G是祖父节点。
在这种情形只有X和P是红色的，G是黑色的，否则就会在插入前有两个相连的红色节点，违反规则。
采用伸展树的术语，X、P和G可以形成一个一字形链或之字形链（两个方向中的任意个方向）。

下图指出P是一个左儿子时我们应该如何旋转该树。即使X是一片树叶，我们还是画出较一般的情形，使得X在树的中间。后面我们将用到这个较一般的旋转。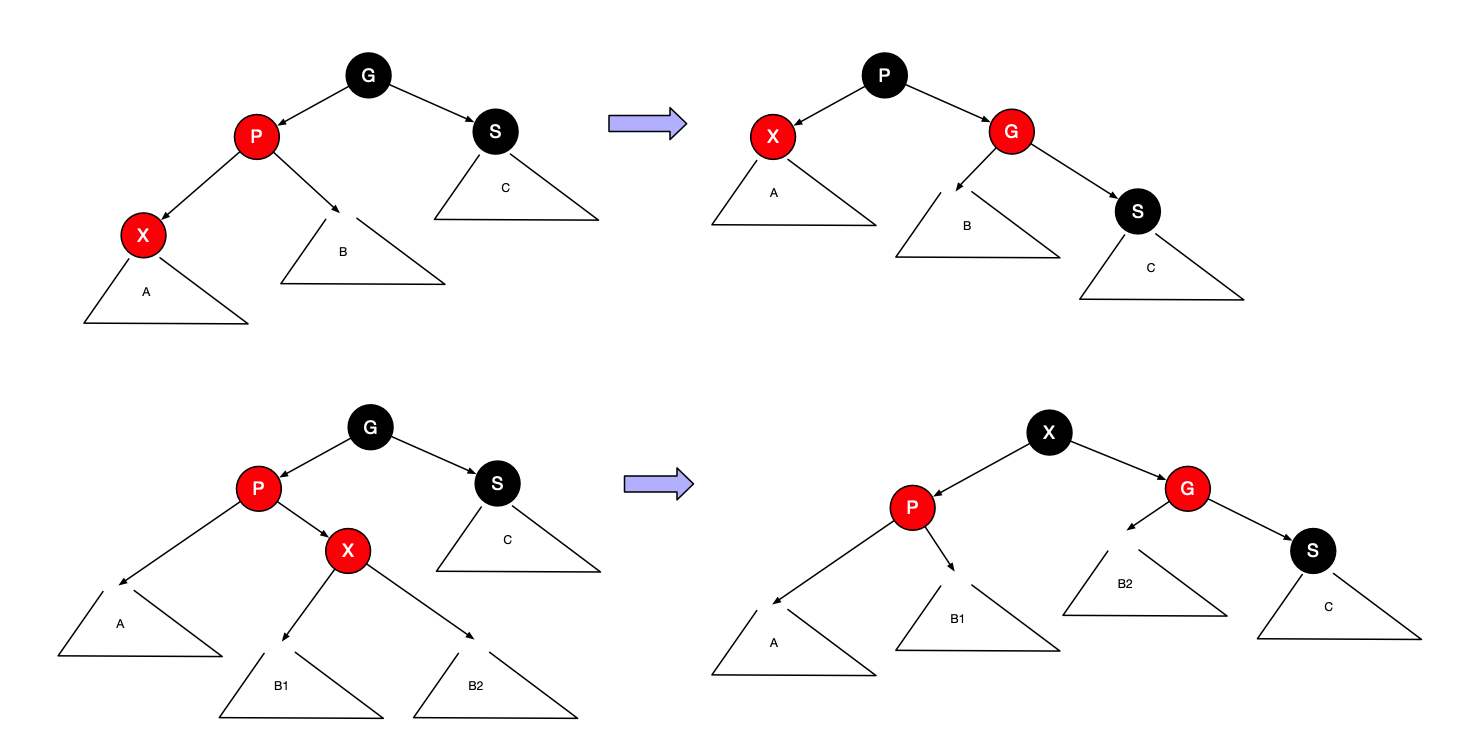
github
如果S是黑色，则单旋转和之字形旋转有效

第一种情形对应P和G之间的单旋转，而第二种情形对应双旋转，该双旋转首先在X和P之间进行，然后在X和G之间进行。当编写程序时，必须记录父节点、祖父节点，以及为了重新连接还要记录曾祖节点。
在这两种情形下，子树的新根均被涂为黑色，因此，即使原来的曾祖时红色，我们也排除了两个相邻红色节点的可能性。同样重要的是，这些旋转的结果是通过A，B和C诸路径上的黑色节点个数保持不变。

自顶向下的红黑树

上面的实现需要用到一个栈或用一些父链保存路径。我们看到，如果使用一个自顶向下的过程，则伸展树会更有效，事实上我们可以对红黑树应用自顶向下的过程而保证S不会是红色的。
这个过程在概念上非常容易。在向下的过程中功能当看到一个节点X有两个红儿子的时候，可使X呈红色而他的两个儿子是黑色的。（如果X是根，则在颜色旋转后他将是红色的，但是为恢复性质2可以直接着成黑色）
下图显示这种颜色反转的现象，只有当X的父节点P也是红色的时候这种反转将破坏红黑的法则。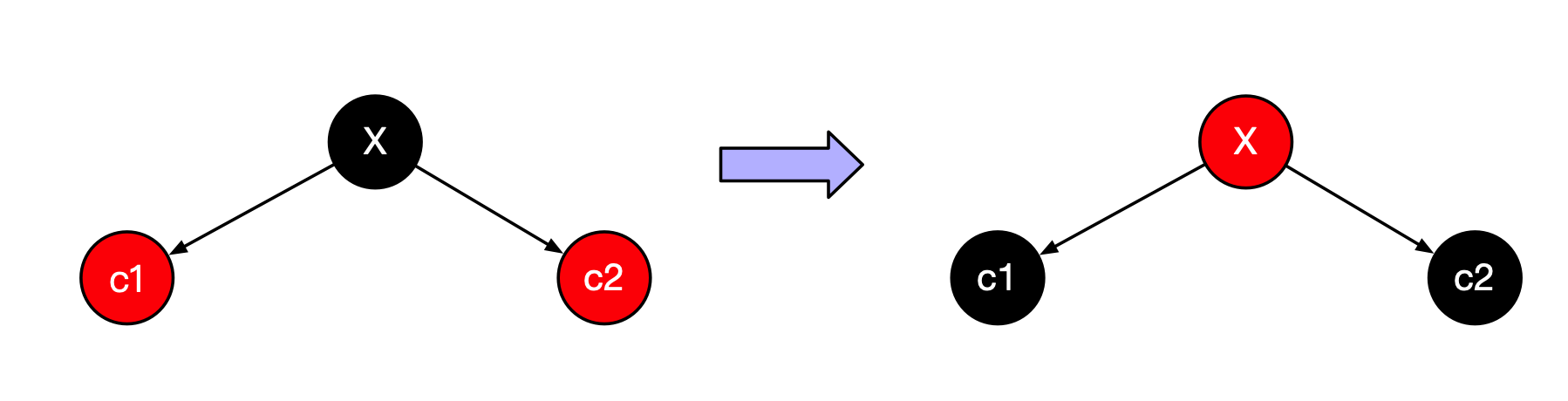
github
颜色翻转：只有当X的父节点是红色的时候我们才能继续旋转。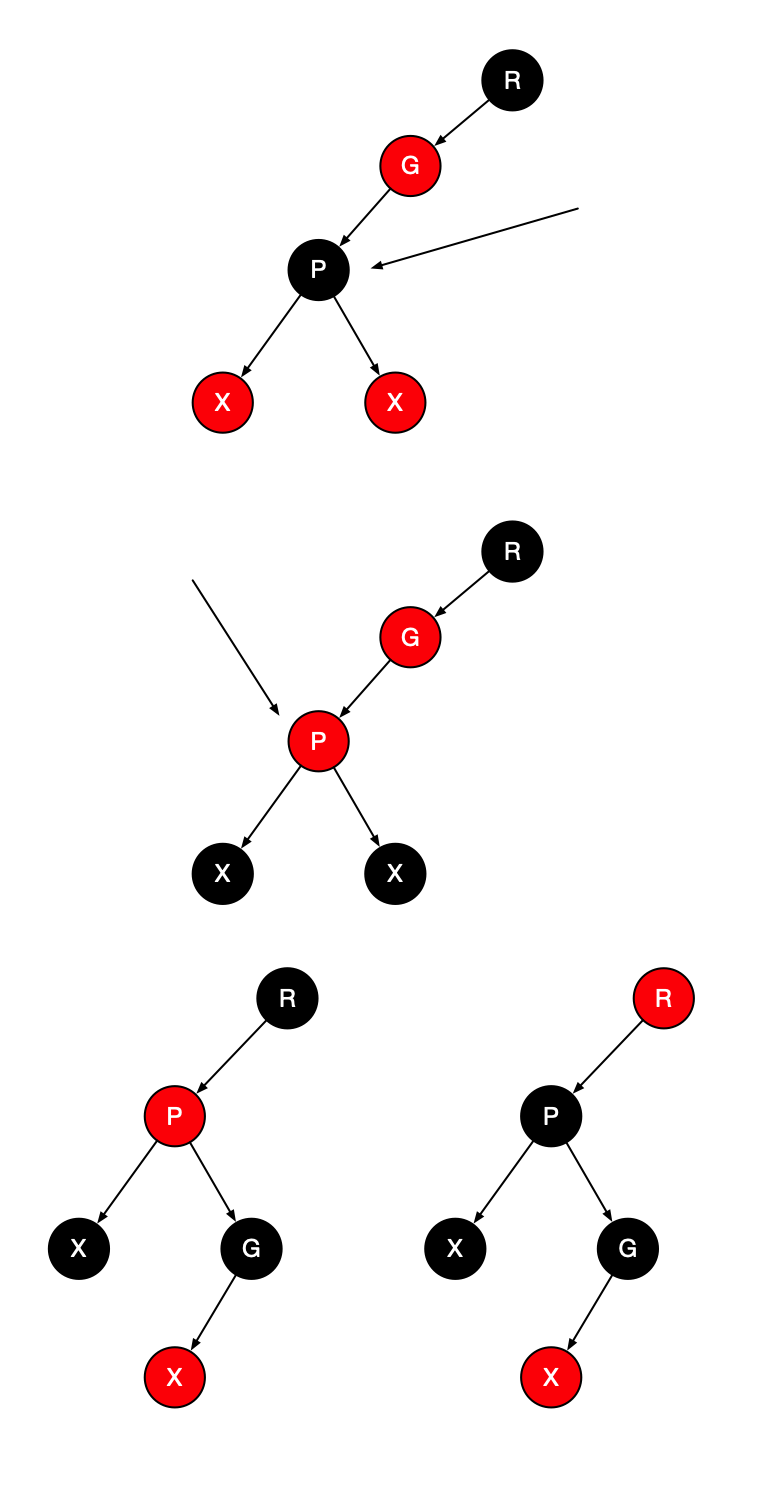
github
此时可以进行适当的旋转。如果X的父节点的兄弟是红色会怎样，这周可能已经被从顶向下过程中的行动所排出，因此X的父节点的兄弟不可能是红色。特别的，如果在延树向下的过程中我们看到一个节点Y有两个红儿子，那么我们知道Y的孙子必然是黑的，由于Y的儿子也要变成黑的，升职在可能发生的旋转之后，因此我们将不会看到两层上另外的红节点。这样我们看到X，若X的父节点是红色的，则X的父节点的兄弟不可能也是红色的。

例如，假设要将45插入到下面的树中。在延树向下的过程中，我们看到50有两个红儿子。因此我们执行一次颜色翻转，使50位红的，40和55为黑的。
现在50和60都是红的，在60和70之间执行单旋转，使得60时30的右子树的黑根，而70和50都是红的。
如果我们在路径上看到另外的含有两个红儿子的节点，那么我们继续执行统一的操作。当我们达到树叶时，把45作为红节点插入，由于父节点使黑的，因此插入完成得到最后的结果。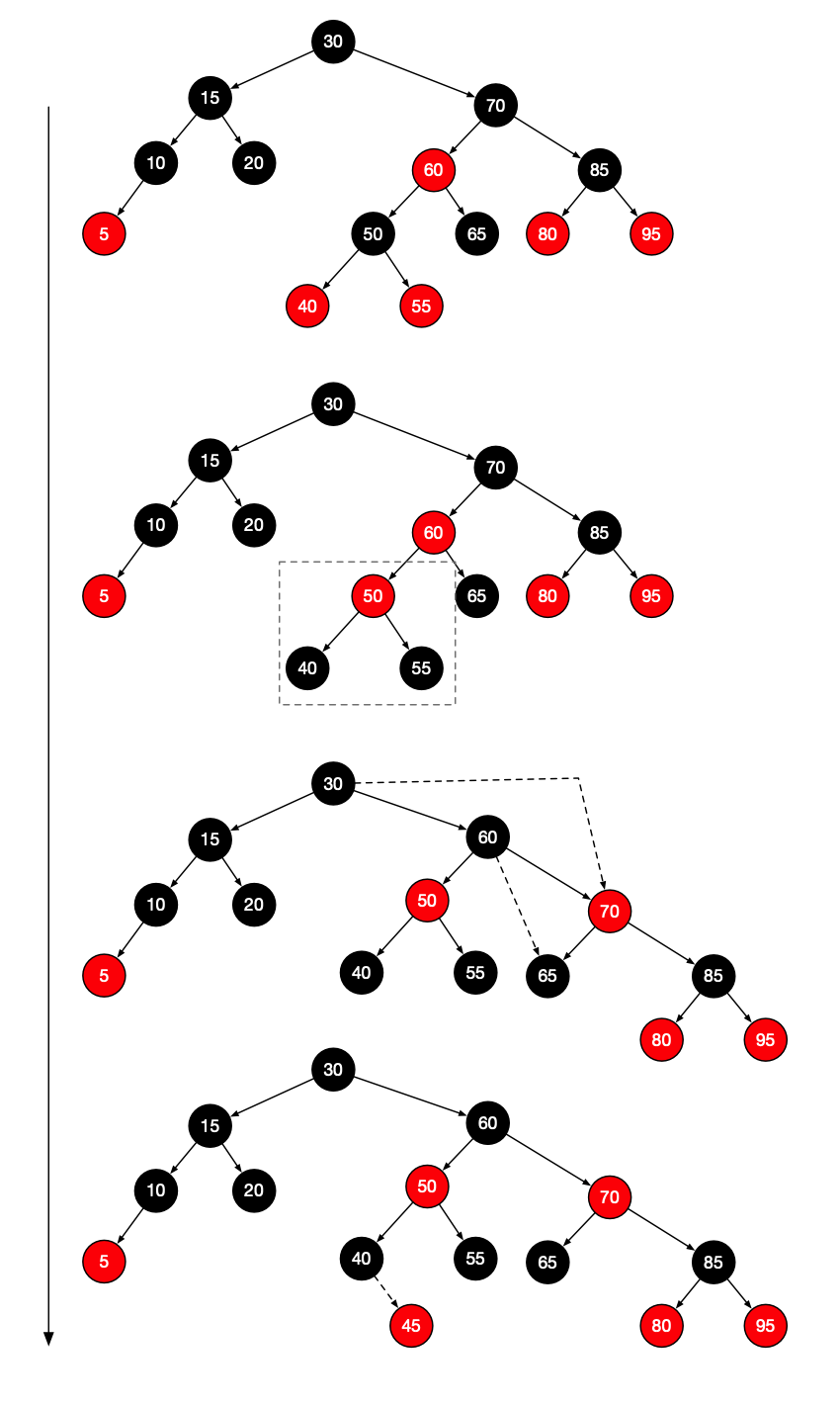
github
最后得到了平衡的红黑树。红黑树的优点是执行插入所需要的开销相对较低，另外就是实践中发生的旋转相对较少。（相较于AVL树）

红黑树的具体实现时很复杂的，这不仅因为有大量可能的旋转，而且还因为一些子树可能是空的，以及处理根的特殊的情况（尤其是根没有父亲）。
因此，我们使用两个标记节点：一个是根，一个是NulNode，他的作用像在伸展树中那样指示一个null引用。根标记将存储关键字∞和一个只想真正的根的右链。
为此，查找和输出过程均需要调整。递归的历程都很巧妙。下面代码中指出如何重新编写中序遍历

public void printTree() {
    if (isEmpty())
        System.out.println("empty tree");
    else
        printTree(header.right);
}

private void printTree(RedBlackNode<AnyType> t) {
    if (t != nullNode) {
        printTree(t.left);
        System.out.println(t.element);
        printTree(t.right);
    }
}

下面代码显示RedBlackTree架构（省去了其中的一些成员方法）以及构造方法。

public class RedBlackTree<AnyType extends Comparable<? super AnyType>> {

    private RedBlackNode<AnyType> header;
    private RedBlackNode<AnyType> nullNode;
    
    private static final int BLACK = 1;
    private static final int RED = 0;

    public RedBlackTree() {
        nullNode = new RedBlackTree<AnyType>(null);
        nullNode.left = nullNode.right = nullNode;
        header = new RedBlackTree<AnyType>(null);
        header.left = header.right = nullNode;
    }
    
    private static class RedBlackNode<AnyType> {
        // 数值
        AnyType element;
        // 左节点
        RedBlackNode<AnyType> left;
        // 右节点
        RedBlackNode<AnyType> right;
        // 颜色
        int color;
    
        RedBlackNode(AnyType theElement) {
            this(theElement, null, null);
        }
    
        RedBlackNode(AnyType theElement, RedBlackNode<AnyType> lt, RedBlackNode<AnyType> rg) {
            element = theElement; left = lt; right = rt; color = RedBlackTree.BLACK;
        }
    }
}

下面则显示执行一次单旋转的例子，因为所得到的数必须要附接到一个父节点上，所以rotate把父节点作为一个参数。我们把item作为一个参数传递而不是在延树下行时记录旋转的类型。
由于期望在插入过程中进行很少的旋转，因此使用这个这种方式实际上不仅更简单，而且还更快。rotate直接返回执行一次适当的单旋转的结果。

private RedBlackNode<AnyType> rotate(AnyType item, RedBlackNode<AnyType> parent) {
    if (compare(item, parent) < 0) 
        return parent.left = compare(item, parent.left) < 0 ?
            rotateWithLeftChild(parent.left) : 
            rotateWithRightChild(parent.left);
    else
        return parent.right = compare(item, parent.right) < 0 ?
            rotateWithLeftChild(parent.right) : 
            rotateWithRightChild(parent.right);
}

private final int compare(AnyType item, RedBlackNode<AnyType> t) {
    if (t == header)
        return 1;
    else 
        return item.compareTo(t.element);
}

下面则给出了插入过程。handleReorient当我们遇到带有两个红儿子的节点时被调用，在我们插入一片树叶时他也被调用。最为复杂的部分时，一个双旋转实际上是两个单旋转，而且只有当通向X的分值（在insert方法中由current表示）去相反方向时才进行。正如我们在较早的讨论中提到的，当延树向下进行的时候，insert必须记录父亲、祖父和曾祖。
由于这些量要由handleReorient共享，因此让他们时类成员。
注意，在一次旋转之后，存储在祖父和饿曾祖父节点中的值将不再正确。不会肯定到下一次在需要他们的时候他将被修复。

private RedBlack<AnyType> current;
private RedBlack<AnyType> parent;
private RedBlack<AnyType> grand;
private RedBlack<AnyType> great;

private void handleReorient(AnyType item) {
    current.color = RED;
    current.left.color = BLACK;
    current.right.color = BLACK;
    if (parent.color == RED) {
        grand.color = RED;
        // 双旋转中的单旋转
        // 判断添加为下面情况则需要进行双旋转
        //          GP
        //        /
        //      P
        //    /    \
        //   C    (item)
        if ((compare(item, grand) < 0) != (compare(item, parent) < 0))
            parent = rotate(item, great);
        // 单旋转
        current = rotate(item, great);
        current.color = BLACK;
    }
    header.right.color = BLACK;
}

public void insert(AnyType item) {
    current = parent = grand = header;
    nullNode.element = item;
    
    while(compare(item, current) != 0) {
        great = grand;
        grand = parent;
        parent = current;
        current = compare(item, current) < 0? current.left : current.right;
        
        // 两个儿子为红色
        if (current.left.color == RED && current.right.color == RED)
            handleReorient(item);
    }
    
    if (current != nullNode) 
        return;
    current = new RedBlackNode<AnyType>(item, nullNode, nullNode);
    
    if (compare(item, parent) < 0)
        parent.left = current;
    else
        parent.right = current;
    // 单旋转
    handleReorient(item);
}

自顶向下的删除

红黑树中的删除也可以自顶向下进行。每一件工作都归结于能够删除树叶。这是因为，要删除一个带有两个儿子的节点，用右子树上的最小节点代替他；该节点必然最多有一个儿子，然后将该节点删除。只有一个右儿子的节点可以用相同的方式删除，而只有一个左儿子的节点通过用其左子树上最大节点替换而被删除，然后再将该节点删除。
注意，对于红黑树，我们不要使用绕过带有一个儿子的节点的情形的方法，因为这可能在树的中部连接两个红色节点，增加红黑条件实现的困难。

当然，红色树叶的删除很简单。但是如果一片黑色树叶，那么删除操作会复杂多，因为黑色节点的删除会破坏规则4.解决方法是保证从上到下删除期间树叶是红色的。
在整个讨论中，令X为当前节点，T是他的兄弟，P是他们的父亲。开始时我们把树的根涂成红色。当延树向下遍历时，我们设法保证X是红色的。当到达一个新的节点时，我们要确信P是红色的并且X和T是黑色的。这存在两个主要的情况。

首先，设定X右两个黑儿子。此时有三种子情况，如下图

如果T也有两个黑儿子，那么可以翻转X、T和P的颜色来保持这种不变形。
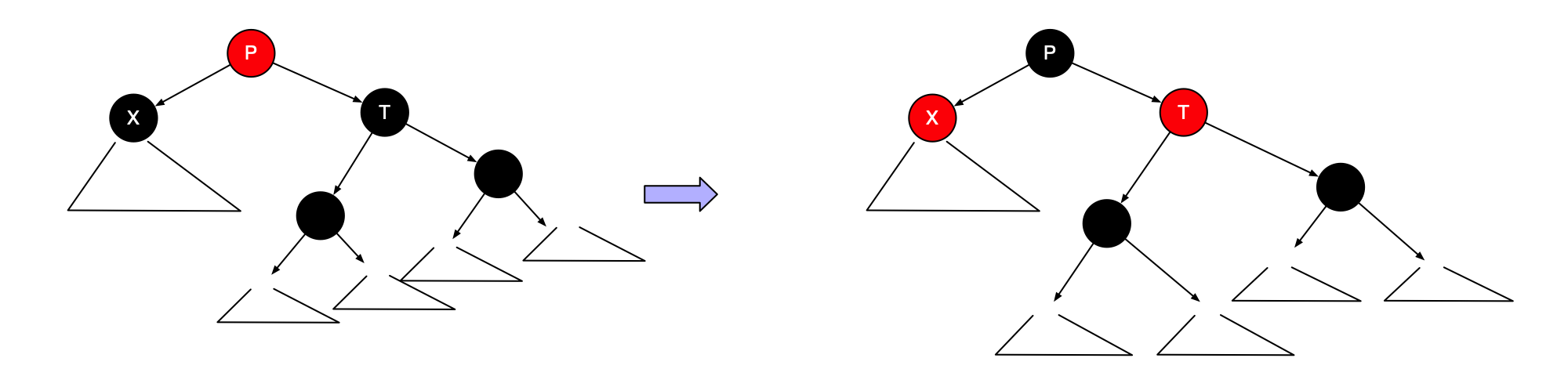
T的儿子之一是红的，根据哪个儿子是红的需要区分哪种旋转，需要特别注意，这种情形对于树叶是适用的，因为nullNode为黑。

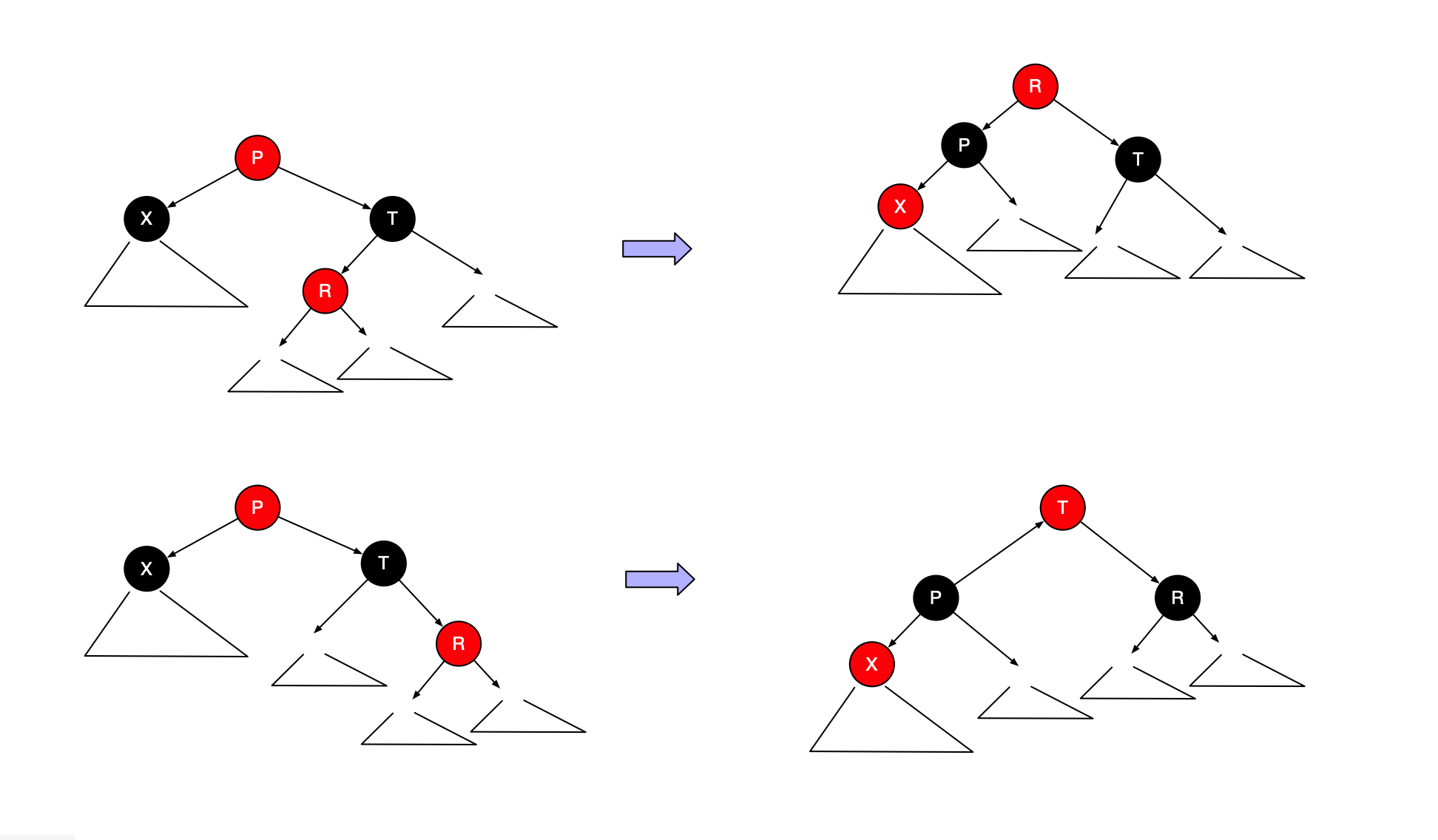
其次，X的儿子之一是红的，在这种情形下，我们落到下一层上，得到新的X、T和P。
如果幸运，X落在的红儿子上，则我们可以继续向前进行。如果不是，那么我们就知道T将是红的，而X和P都将是黑的。我们就可以旋转T和P，使得X的新父亲是红的；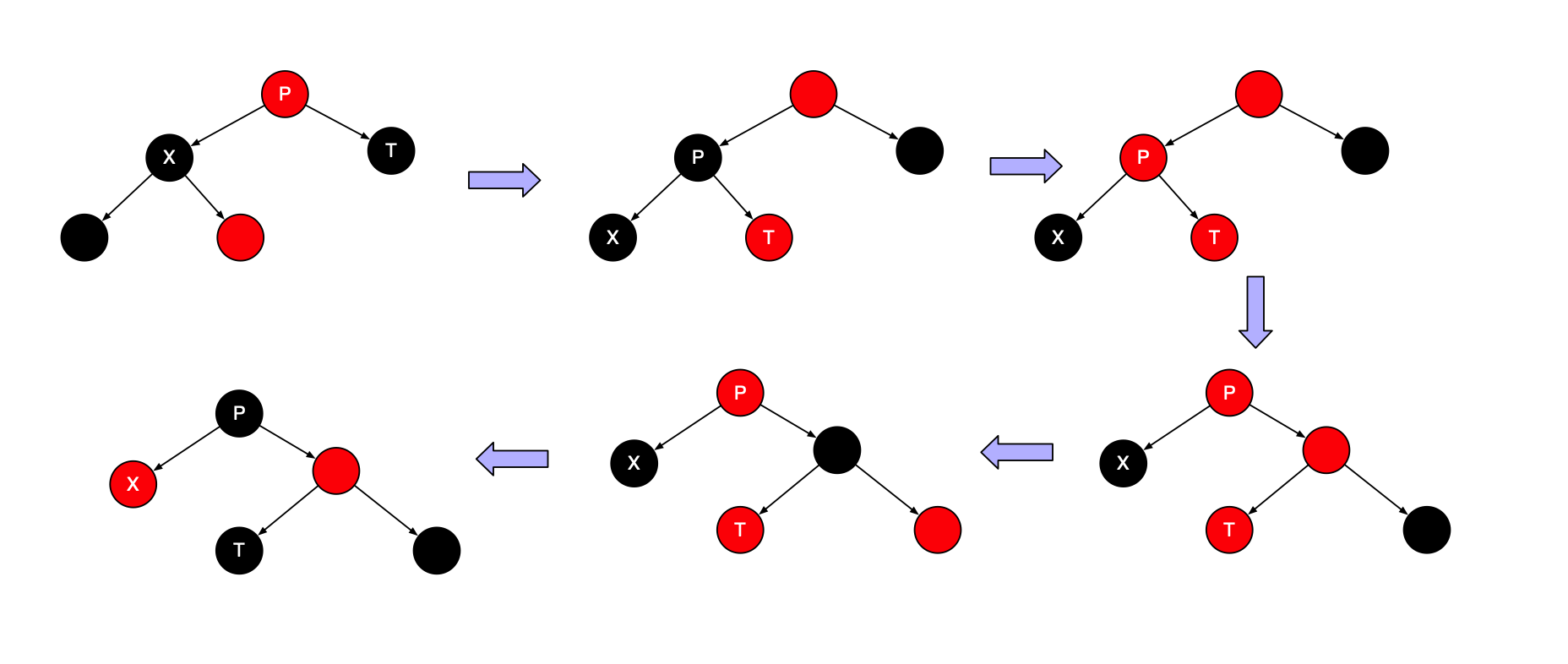
github

下坠
变换
旋转
根据规则变色
颜色反转
删除

确定性跳跃表

用于红黑树的一些想法可以应用到跳跃表以保证对数最坏情况操作。这里我们描述所得到数据结构的最简单的实现方法，1-2-3确定性跳跃表。
跳跃表中的节点随机指定了高度。高度为h的节点包含h个前向链p1,p2,p3…Ph,Pi链接到高度为i或更大的下一个节点。一个节点具有高度h的概率为0.5^h(为了实现时/空交换，0.5可以用0到1.0之间的任何数来代替)。因此，我们期望只处理一些前向链直到下降一层；由于有大约logN层，因此我们得到每次操作花费O(logN)的期望运行时间。
为使这个界称为最坏情形的界，我们需要保证只有常数个前向链从一个元素指向另一个元素。
定义1：两个元素称为是链接的，如果至少存在一个链从一个元素指向另一个元素。
定义2：两个在高度h上连接的元素间的间隙容量等于他们之间高度为h-1的元素数量

1-2-3确定性跳跃表满足一下性质：每一个间隙（除在头和尾之间）的容量为1、2或3。
例如下图，显示了一个1-2-3确定性跳跃表。该表有两个容量为3的间隙；第一个是35和45之间有高度为1的三个元素，第二个是在表头和表尾之间有高度为2的三个元素。尾节点包含∞，他的出现简化了算法并使得定义表终端间隙的概念更容易。
github

显然，沿任一层行进仅仅通过常数个链就可以下降到低一层。因此，在最坏的情形下查找的时间是O(log N)。
为了执行插入，我们必须保证当一个高度为h的新节点加入进来不会产生具有4个高度为h的节点间隙。实际上很简单，我们采用类似于在红黑树中所做的自顶向下的策略即可。

设我们在L层上，并正要降到下一层去。如果要降到的间隙容量是3，那么我们提高该间隙的中间项使其高度为L，从而形成两个容量为1的间隙。由于这使得朝向插入的道路上消除了容量为3的间隙，因此插入是安全的。

例如下面将27插入到表中。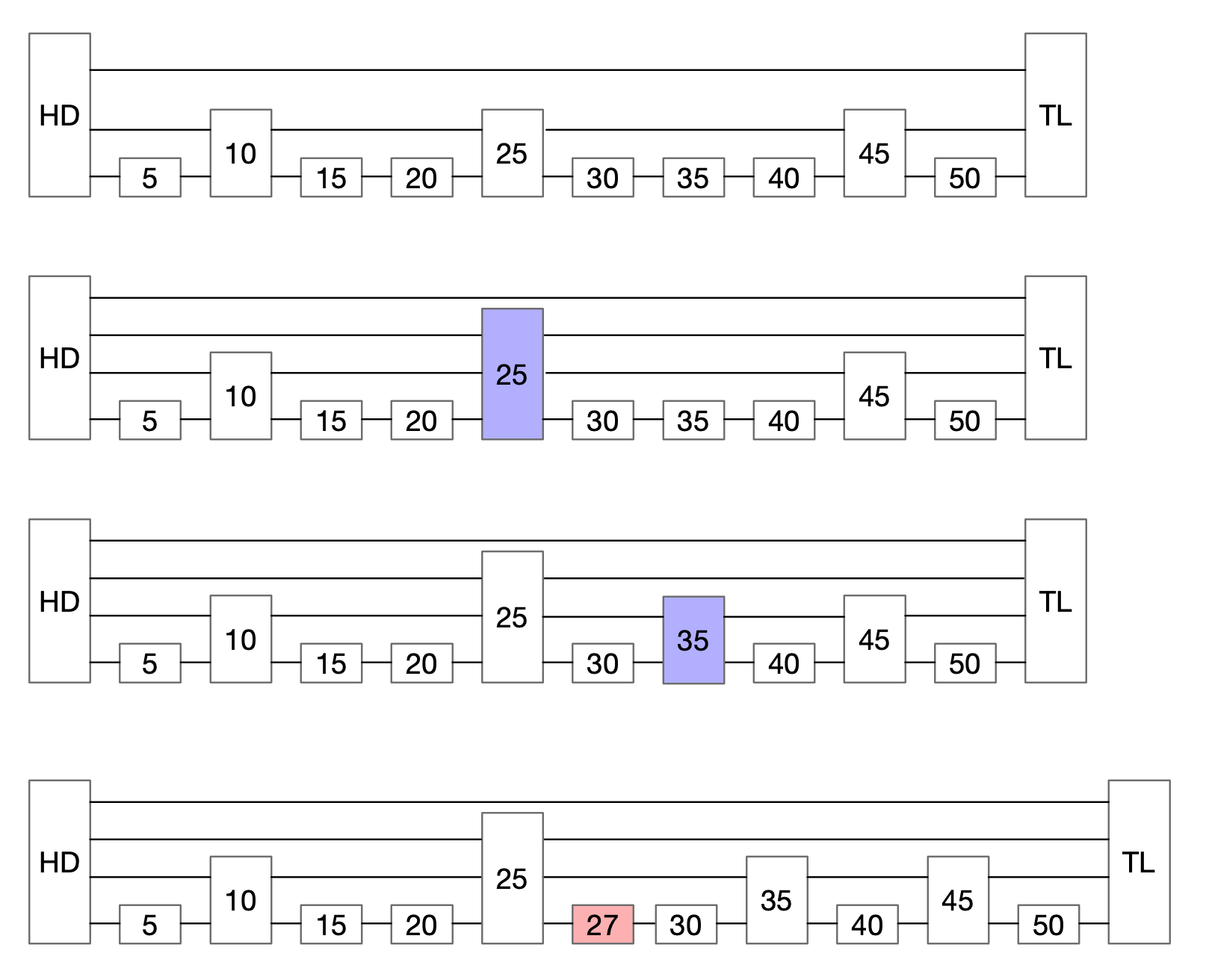
github

从第三层降到第二层
由于降落到容量为3的间隙，因此这里需要将中间项上升到3的高度，并在表中拼接。
下降到第一层，又见到容量为3的间隙，因此把35提升到高度2
最后插入到表中。

删除的困难是出现在间隙容量为1的情况。当我们看到将要下降到一个容量为1的间隙时，我们要把这个间隙放大，或者是通过从相邻间隙（如果容量不为1）借来的方式，或者通过将该间隙与邻间隙分开的节点的高度降低的方式。由于这两个都是容量为1的间隙，因此结果变成容量为3的间隙。由于有几种情况要处理，因此程序比我们的描述稍微复杂一点。
第一个重要的细节是，当我们将一个高h的节点提升到高h+1的时候，我们不能花费时间O(h)用来奖h个链拷贝到一个新数组。否则插入的时间就要成为O(log^2 N)。一种方法是用一个链表来表示高度为h的节点中的h个前向链。由于我们是沿着各层向下进行，因此一个节点的链表是以第h层前向链开始并以第一层前向链结束
第二个优化更复杂且可能占用更多的空间。我们不是把节点作为一项和前向链的链表来存储，而且是存储前向链和前向项对的链表。理解其含义的最容易的方法是下图，我们将使用术语抽象或逻辑来表示。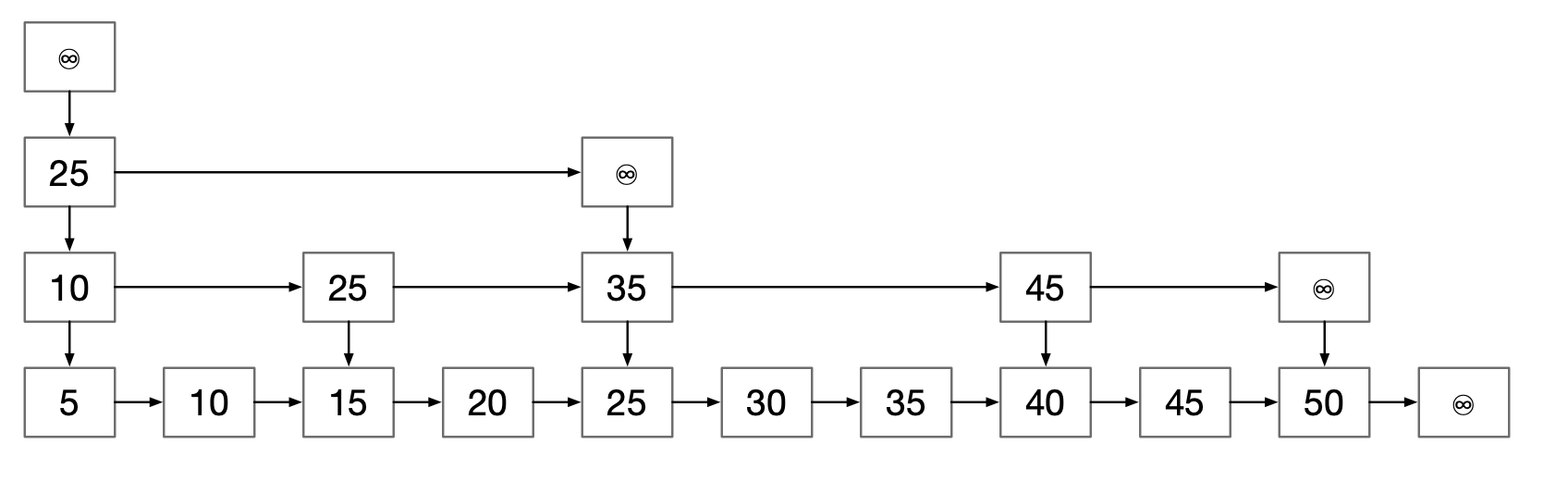
github

注意，除了尾节点被删除外，抽象表示和实际实现二者的地平线是一样的。我们的实现中，每一个节点都留有使我们下降一层的链，指向同层上的下一个节点的链以及逻辑上存储在下一项中的项。
有些项的出现是多于一次的。例如25出现了三个地方。事实上，如果一个节点在抽象表示中的高度为h，那么他的项在实际实现中就会出现h个地方。部分重要的结论和结果需要在实现方法后进行解释。
基本节点由一个项和两个链组成。为了使编程更快更简单，我们使用了尾节点。如果不能够或不希望赋值♾，那么就必须使用其他方式。

我们对头节点和底层节点都有一个标记以代替null链。SkipNode类和DSL构造方法如下：

public class DSL<AnyType extends Comparable<? super AnyType>> {
    public DSL(AnyType inf) {
        infinity = inf;
        bottom = new SkipNode<AnyType>(null);
        bottom.right = bottom.down = bottom;
        tail = new SkipNode<AnyType>(infinity);
        tail.right = tail;
        header = new SkipNode<AnyType>(infinity, tail, bottom);
    }
    
    private static class SkipNode<AnyType> {
        SkipNode(AnyType theElement) {
            this(theElement, null, null);
        }
        
        SkipNode(AnyType theElement, SkipNode<AnyType> rt, SkipNode<AnyType> dt) {
            element = theElement;
            right = rt;
            down = dt;
        }
        
        AnyType element;
        SkipNode<AnyType> right;
        SkipNode<AnyType> down;
    }
    
    private AnyType infinity;
    
    private SkipNode<AnyType> header;
    private SkipNode<AnyType> bottom = null;
    private SkipNode<AnyType> tail = null;
    
}

查找函数与随机化跳跃表的查找函数相同。下面代码中如果我们得不到匹配的项，那么或者向下进行，或者向右进行，这依赖于比较的结果。

public boolean contains(AnyType x) {
    SkipNode<AnyType> current = header;
    bottom.element = x;
    for( ; ; ) {
        int compareResult = x.compareTo(current.element);
        if (compareResult < 0)
            current = current.down
        else if (compareResult > 0)
            current = current.right
        else 
            return current != bottom
    }
}

下面则是插入操作，由于标记的引入而大大的得到简化。利用某些繁琐的链跟踪可以看到，如果对每一个链是否是null进行测试，那么可能将代码扩大三倍。

public void insert(AnyType x) {
    SkipNode<AnyType> current = header;
    
    bootom.element = x;
    while(current != bottom) {
        while(current.element.compareTo(x) < 0)
            current = current.right;
            
        if (current.down.right.right.element.compareTo(current.elemenmt) < 0) {
            current.right = new SkipNode<AnyType>(current.element, current.right, current.down.right.right);
            current.element = current.down.right.element;
        } else {
            current = current.down;
        }
    }
    
    if (header.right != tail)
        header = new SkipNode<AnyType>(infinity, tail, header);
}

确定性跳跃表插入过程的程序多少要短一些，考虑的情况比红黑树少得多。我们所付出的代价只有空间：在最坏情况下我们有2N个节点，每一个节点包含两个链和一个项。
对于红黑树，我们有N个节点，每一个节点包含两个链、一项以及一个颜色位。因此我们可能要用两倍多的空间。经验指出确定性跳跃表平均使用1.57N个节点，其次某些情况下，确定性跳跃表实际使用的空间少于红黑树。

有一个适用于C/C++的实际例子。在32位机器上，链和整数是4个字节。对于某些系统，包括某些UNIX，内存时按块(chunk)来培植的，他们通常是2的幂，但存储管理程序使用4个字节的块。于是对于12个字节的请求将得到一个16字节块，即12个字节用户使用而剩下4个字节作为系统开销。
但是对于13个字节的需求则必须提供一个32字节块。因此，这种情况下，确定性跳跃表每个节点使用16个字节，而平均有1.57个N，因此总数一般有25N个字节。可是红黑树却使用32N个字节。这说明在某些机器上一个附加位(bit)是非常昂贵的。这是自组织结构的吸引力之一。

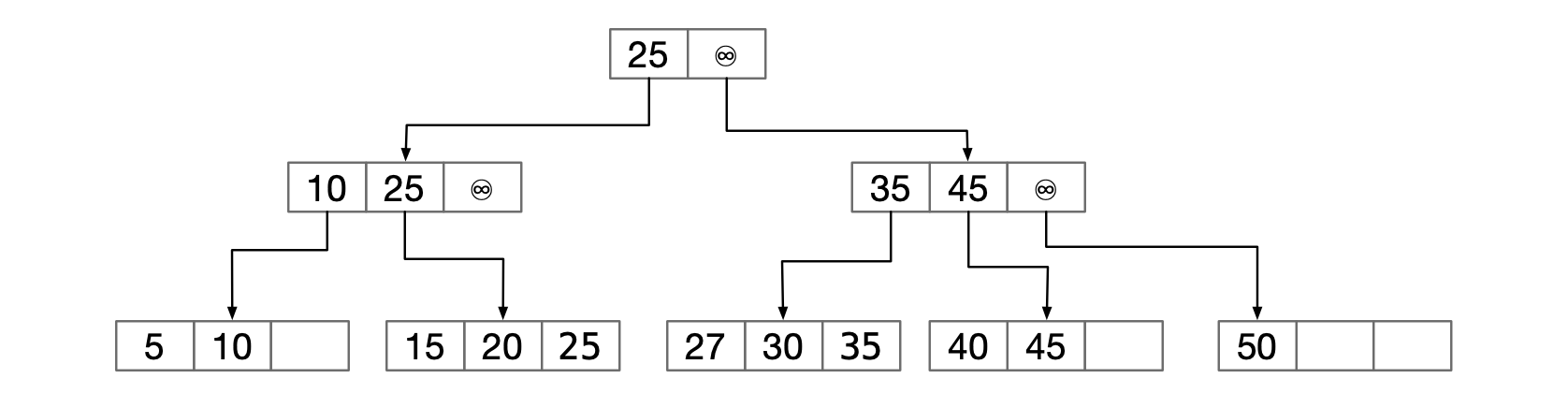
github
确定性跳跃表的性能似乎比红黑树要强。当寻找插入时间的改进时，下面代码包含有逻辑测试：
if (current.down.right.right.element.compareTo(current.elemenmt) < 0)
如果我们把一些项存储在最多三个元素的一个数组中，那么对于第三项的访问可以直接进行，而不用再通过两个right链。上面图中所表示的结构，具有讽刺意味的是，这个结构很像B-树。称之为1-2-3确定性跳跃表的水平数组实现。