一、基本介绍
熵来自与热力学,用于度量能量退化的指标,熵越高,物体的做功能力越低。在信息论中,用于表示消息的平均信息量。信源的熵通常表示所发出信息的不确定性,越是随机的、前后不相关的信息,熵越高。
二、K阶指数哥伦布编码
以指数哥伦布编码为例:
编码过程
设非负整数 x,阶数为k
- 1.将 x 转为2进制 y (若不足k位,高位补0)
- 2.将数值 y 其 k 位后数据去除并保存至 k1,保留下来的数据 加上1, 得 y1(若刚好为 k 为,去掉 k 位后为0)
- 3.M为二进制y1的位数 -1
- 4.在 y1 高位添加 M个0 得 y2
- 5.在 y2 低位添加之前的 k1 得到新二进制 z
z则是编码后数据
指数哥伦布编码后的形式为[MZeors][1][Info]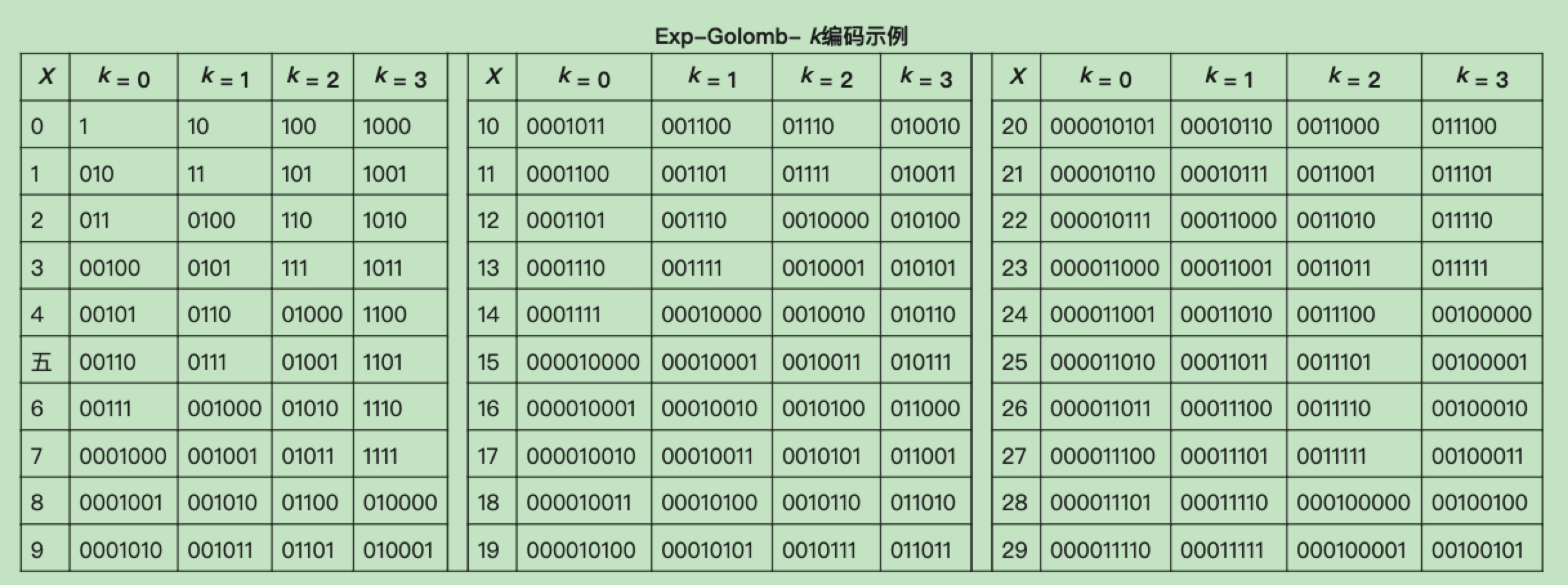
实例1:
x = 10,k = 0
- 1.得到二进制y = 1010
- 2.去除k = 0阶后得到1010,加上1为1011,数据得到y1 = 1011
- 3.位数4,减1得M = 3
- 4.增加至高位得y2 = 000 1011
- 5.添加至低位的z = 000 1011
得到z = 0001011
实例2:
x = 10,k = 3
- 1.得到二进制y = 1010
- 2.去除k = 3阶后得到1,k1 = 010,保留下来的数据 加上1,得到y1 = 10
- 3.M = 2-1 = 1
- 4.在 y1 = 10 的高位添加 M = 1 个0,得到 y2 = 010
- 5.在 y2 = 010 的低位添加 k1 = 010,得到 z = 010 010
得到z = 010010
解码过程
设置得到的二进制码位 x,阶数位k
- 1.连续的0的个数 M
- 2.总长度 len = 2M + k + 1,有效长度 len-H = M + k + 1
- 3.得到读取的有效数据 W 等于有效长度 len-H 下的二进制转十进制数据
- 4.结果数据 z = W - 2^k
z则是解码后数据
在使用K阶哥伦布编码时,可以根据需要来对K做相应调整。
如果在二进制中0出现概率较大,则使用 k = 0
如果在二进制中0和1出现概率都比较大,那么用 k = 1
…
三、哈夫曼编码
哈夫曼编码是变长编码方法的一种,该方法完全依赖于码字出现的概率来构造整体平均长度最短的编码方法。进行哈夫曼编码的关键步骤是建立符合哈夫曼编码规则的二叉树,该树又称作哈夫曼树。
哈夫曼树是一种特殊的二叉树,其终端节点的个数与待编码的码元的个数等同,而且每个终端节点上都带有各自的权值。每个终端节点的路径长度乘以该节点的权值的总和称为整个二叉树的加权路径长度。在满足条件的各种二叉树中,该路径长度最短的二叉树即为哈夫曼树。
哈夫曼编码,主要目的是根据使用频率来最大化节省字符(编码)的存储空间。
编码过程
假设有A、B、C、D、E五个字符,出现的频率(权值)分别为5、4、3、2、1。
- 1.获取最小的两个权值作为左右子树构造一个新树,3为虚线表示该节点为新生成的节点。
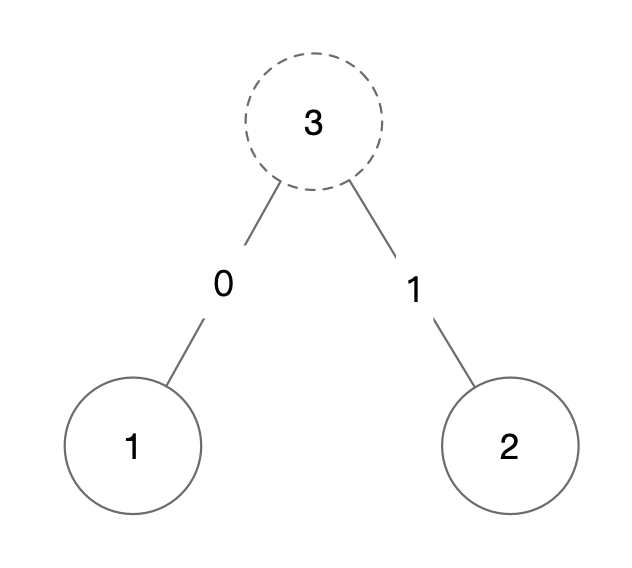
- 2.在第一步的基础上将节点3添加进去,这里注意是将其添加到1中创建的树上。
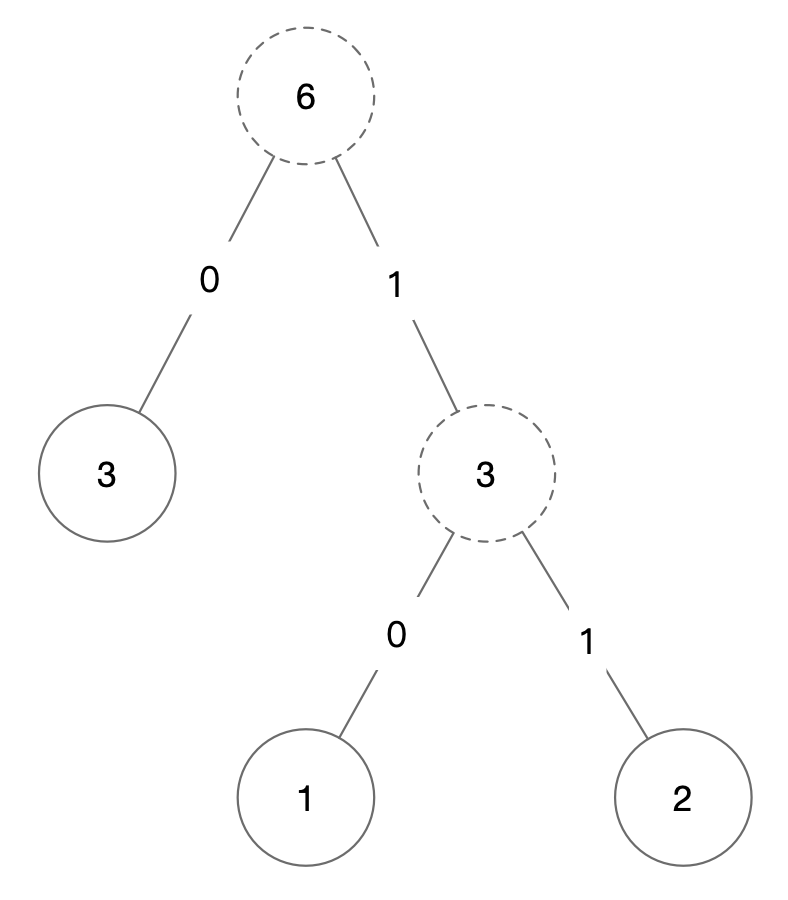
- 3.最后将4、5创建的树添加到2中创建的树上。
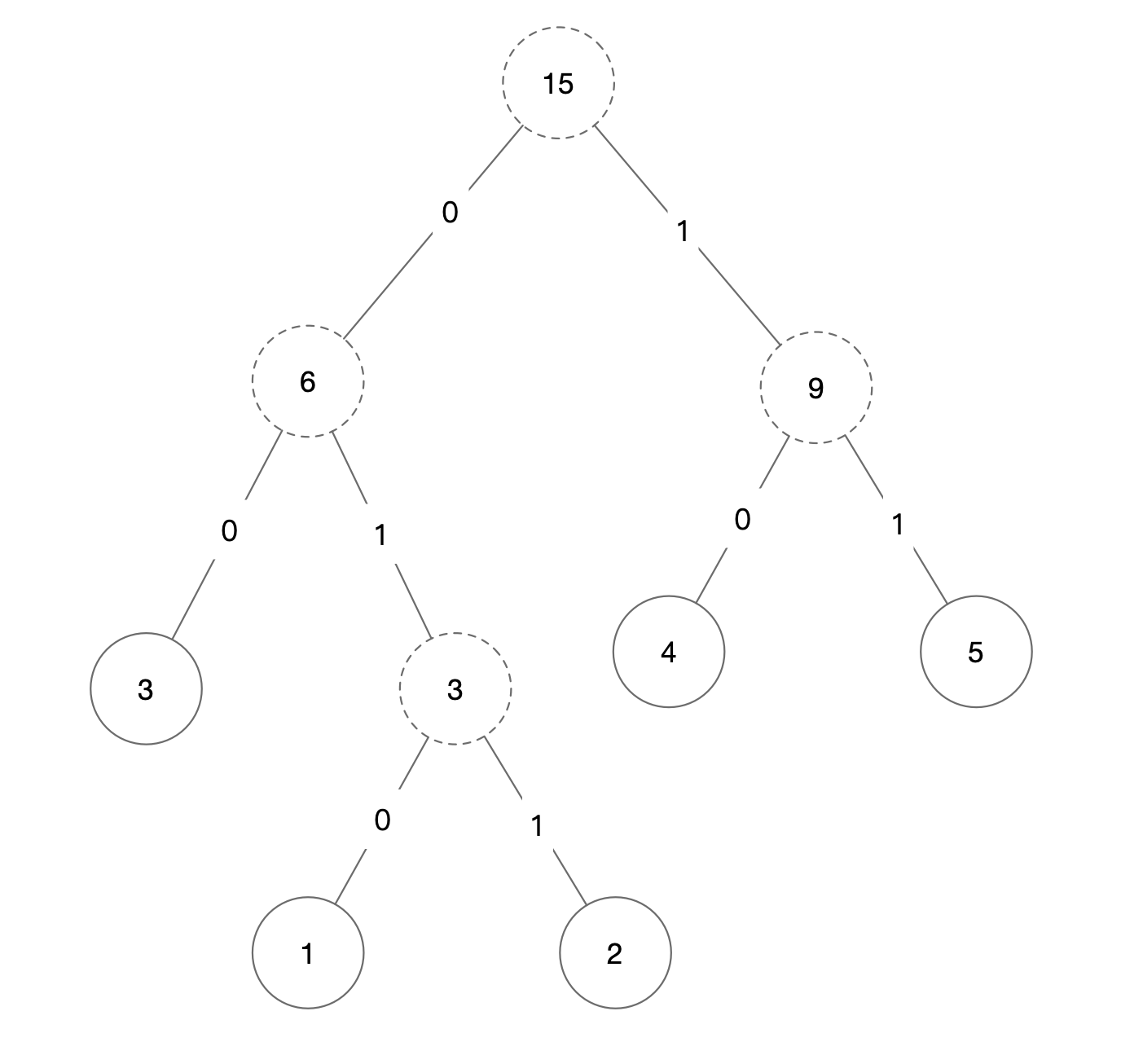
- 4.将响应的权值改为字符。
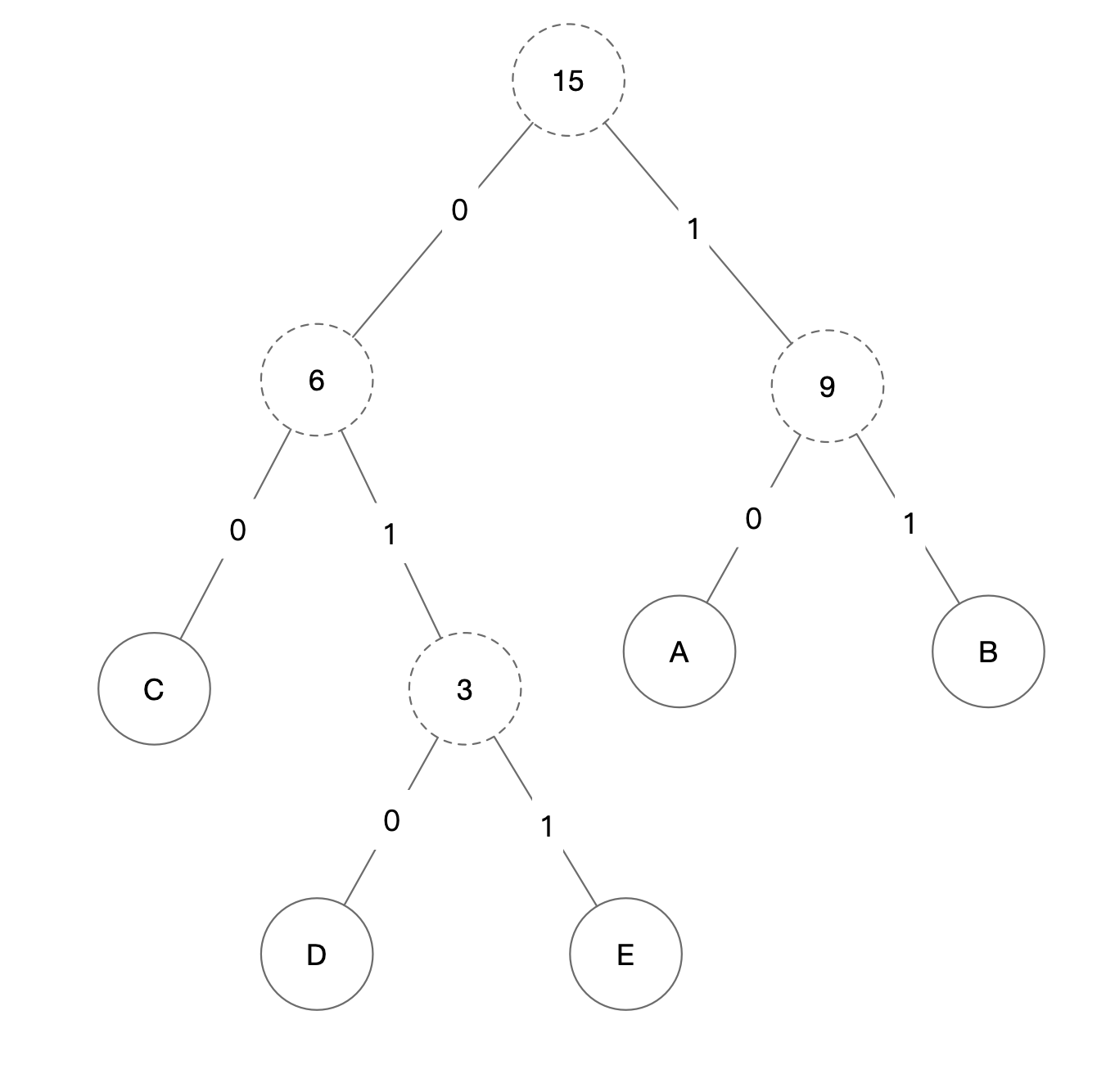
- 5.根据4中修改的树,将对应字符的编码写出。
A:10
B:11
C:00
D:010
E:011
霍夫曼编码是一种无前缀编码。解码时不会混淆。其主要应用在数据压缩,加密解密等场合。